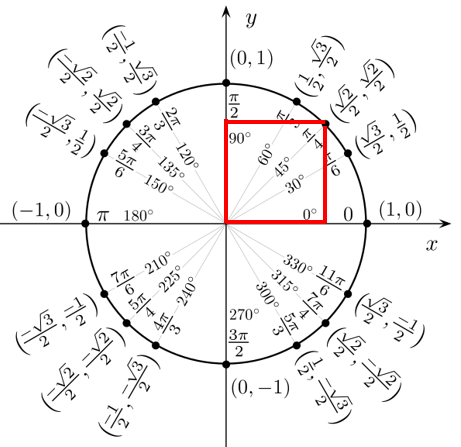
Nel seguente prospetto possiamo analizzare tutti gli angoli notevoli della circonferenza, con i valori corrispondenti di seno e coseno (la tangente si ricava facilmente facendo il seno diviso il coseno).

Il coseno è l’ascissa del punto di intersezione P tra il raggio e la circonferenza e il seno ne è l’ordinata.
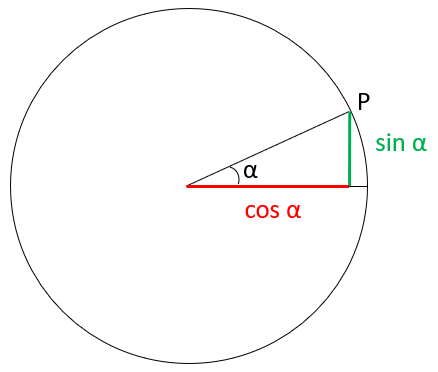
Dalla relazione goniometrica, che collega seno e coseno, è chiaro che all’aumentare del seno il coseno diminuisce e viceversa.
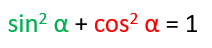
Nel seguente video si vede come variano queste due grandezze in modo dinamico.
Gli angoli notevoli sono 0° (0 radianti), 90° (mezzo radiante), 180° (1 radiante), 270° (1 radiante e mezzo) e 360° (2 radianti, posizione coincidente con quella a 0 radianti), inoltre ci sono quarti, i terzi e i sesti di radiante.
I mezzi radianti si ottengono dividendo ogni radiante in 2 parti (cioè in ciascuno dei 4 quadranti) il che equivale a dividere l’angolo giro in 4 angoli retti.
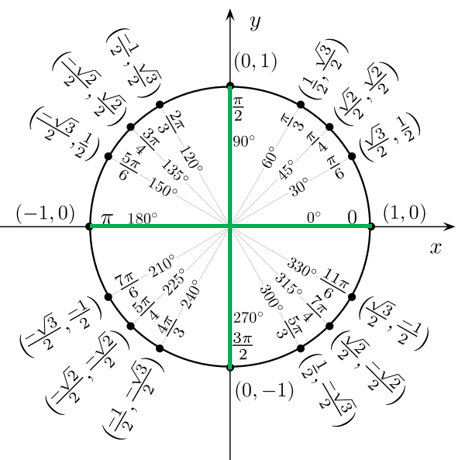
I quarti di radiante si ottengono dividendo ogni radiante in 4 parti (cioè ciascuno dei 4 quadranti del piano cartesiano in due parti uguali) il che equivale a dividere i 4 angoli retti, che insieme compongono un angolo giro, ognuno in due angoli da 45°.
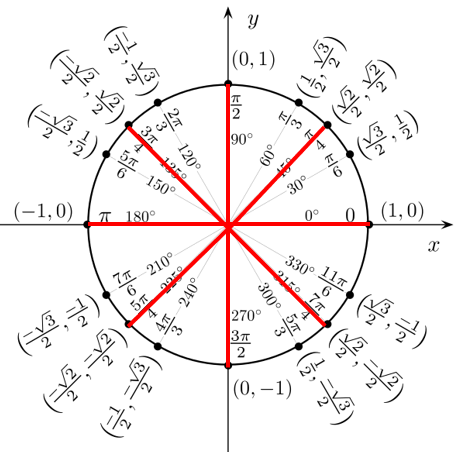
I terzi di radiante si ottengono in modo simile, dividendo ogni radiante in 3 parti.
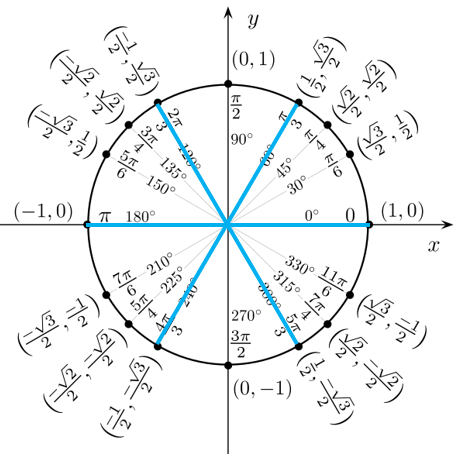
I sesti di radiante si ottengono in modo simile, dividendo ogni radiante in 6 parti.
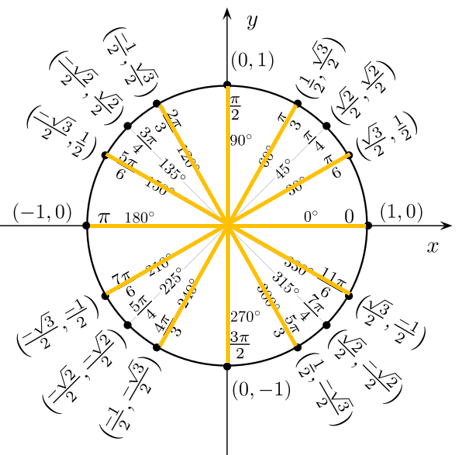
Questo sistema aiuta ad individuare gli angoli contando i mezzi, i quarti, i terzi o i sesti, ad esempio se voglio rappresentare 5/3 π uso questa rappresentazione:
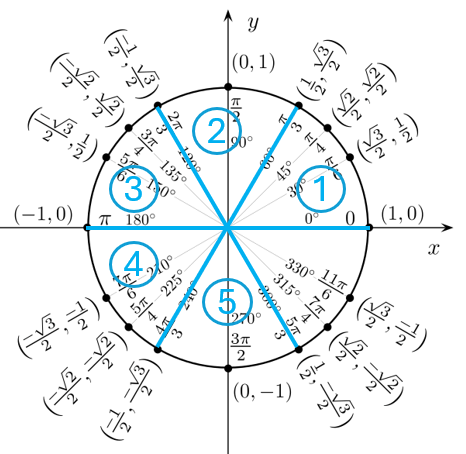
Inoltre, per memorizzare i valori dei seni e dei coseni degli angoli notevoli, è utile ricordare le seguenti rappresentazioni e poi assegnare il segno giusto a seconda del quadrante dove ci si trova:
- nei rettangoli formati dai terzi e dai sesti, il lato corto misura 1/2 e il lato lungo misura √3/2:
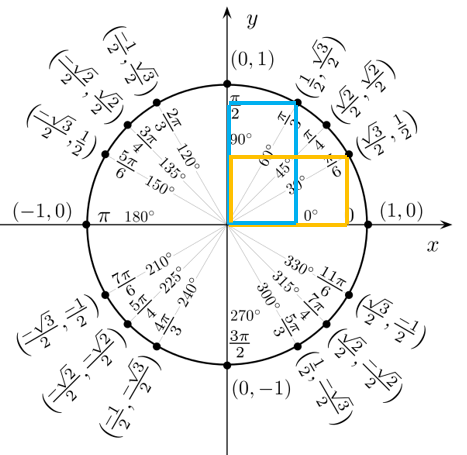
- i quarti, invece, formano dei quadrati i cui lati misurano tutti √2/2:
SCHEMI PER LA RISOLUZIONE DEI TRIANGOLI


