Un polinomio può essere scomponibile in diversi fattori, così come i numeri.
Se, ad esempio, possiamo affermare che 6 sia scomponibile nei due numeri 2 e 3, in quanto 6=2×3, allo stesso modo possiamo pensare che un polinomio sia scomponibile in altri polinomi, provando che è il prodotto tra un polinomio e un altro:
P(x)=Q(x) * D(x)
Se D(x) è un binomio, allora si presenterà nella forma D(x)=x-f, dove f è una radice (o zero) del polinomio, cioè un valore per cui il polinomio si annulla: infatti, f rende nullo uno dei fattori del polinomio e quindi, per la legge di annullamento del prodotto, rende nullo tutto il polinomio.
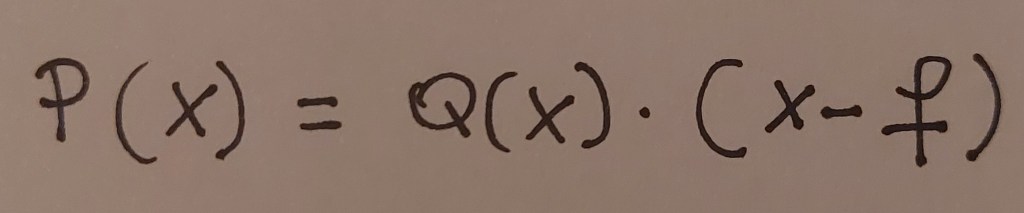
Ad esempio, se f=2, succede questo:
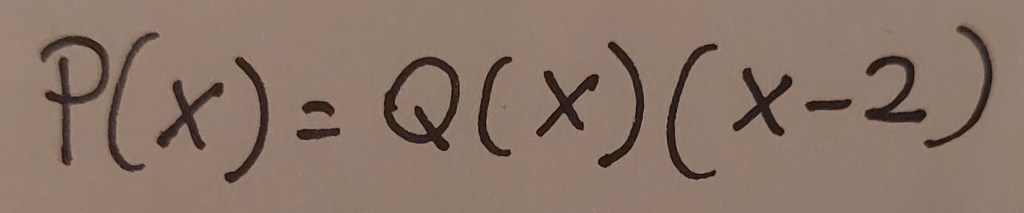
Se x=2 il termine fra parentesi si annulla:
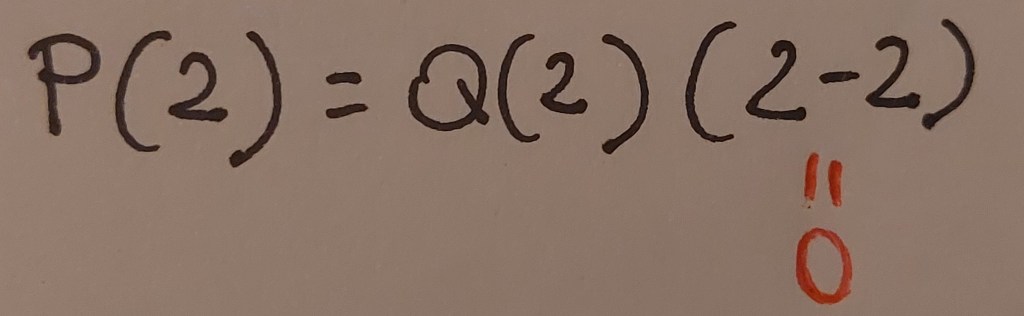
Il fatto che si annulli uno dei fattori fa sì che si annulli tutto il polinomio, quindi P(2)=0.
L’enunciato del teorema di Ruffini afferma infatti che condizione necessaria e sufficiente affinché un polinomio P(x) sia divisibile per un binomio del tipo (x-f) è che P(f) sia uguale a zero, quindi una volta che abbiamo trovato una radice (o zero) f del polinomio allora possiamo effettuare la divisione per (x-f) ottenendo un resto pari a zero.
Ruffini ci dice anche che le radici (o zeri) del polinomio si trovano tra i possibili quozienti tra i divisori del termine noto e quelli del termine di grado massimo.
Nel seguente polinomio il termine di grado massimo è 1, quindi possiamo considerare solo i divisori del termine noto 9.
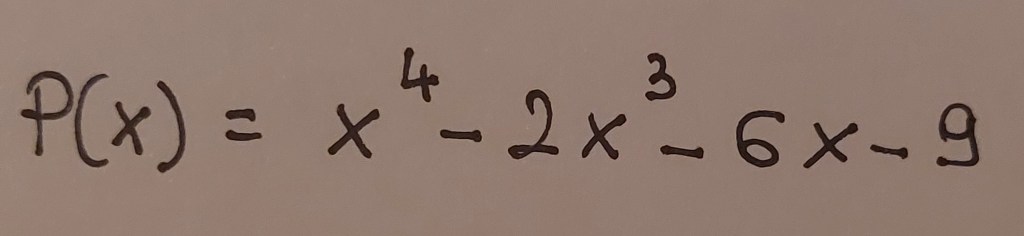
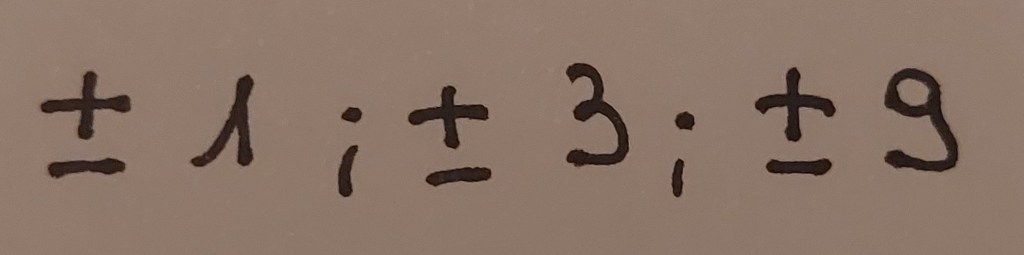
Attenzione però: non tutti i termini così individuati sono radici del polinomio: per trovare quelli che sono davvero radici dobbiamo trovare, per tentativi, quali di essi se si sostituiscono alla x fanno sì che il polinomio diventi zero.
Iniziamo a fare il primo tentativo sostituendo 1:
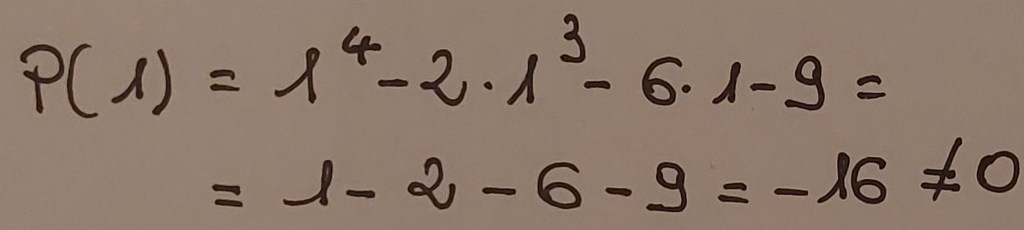
1 non annulla il polinomio, quindi proviamo con -1
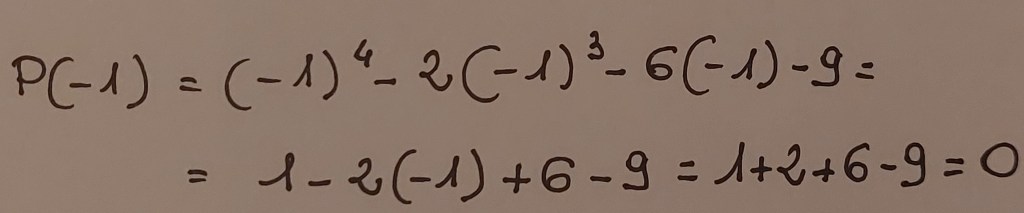
-1 annulla il polinomio, quindi possiamo essere sicuri che il polinomio può essere scomposto così:
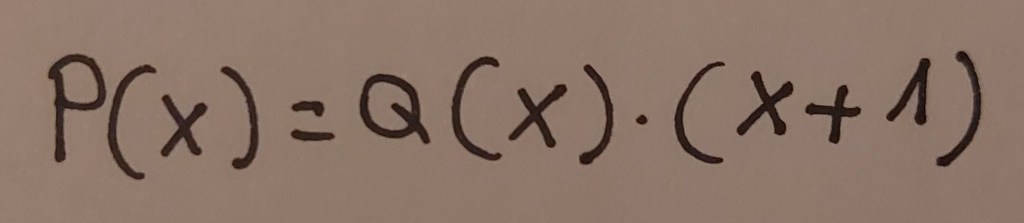
Per scoprire che polinomio è Q(x) possiamo fare la divisione di P(x) per (x+1) con Ruffini.
Partiamo ora invece da un altro polinomio, che ha radice 1 (13 +2*1-3=1+2-3=0)
Per scomporlo lo dovrò dividere per (x-1):
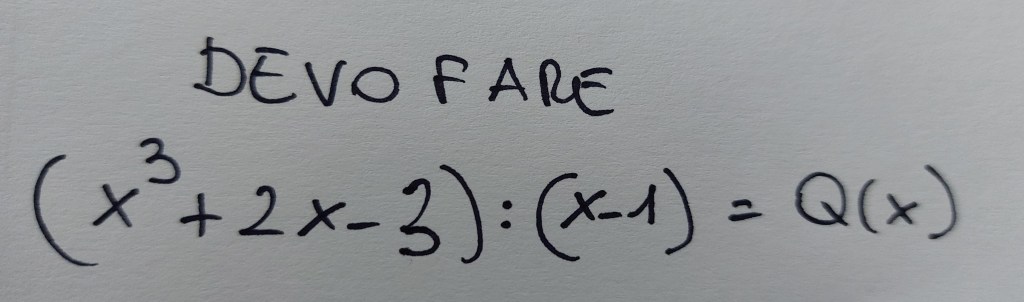
Cioè:
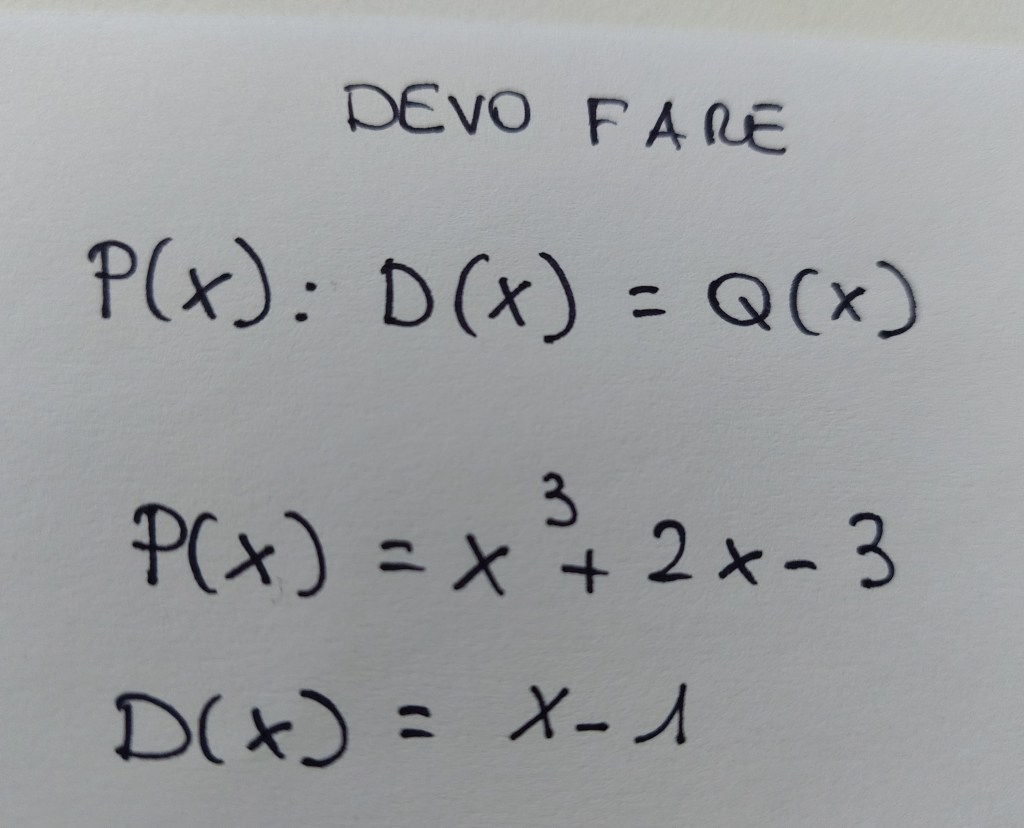
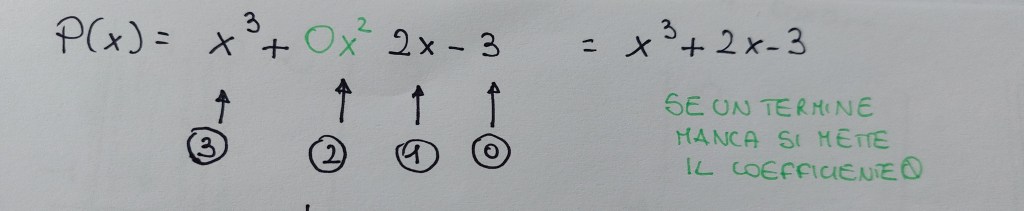
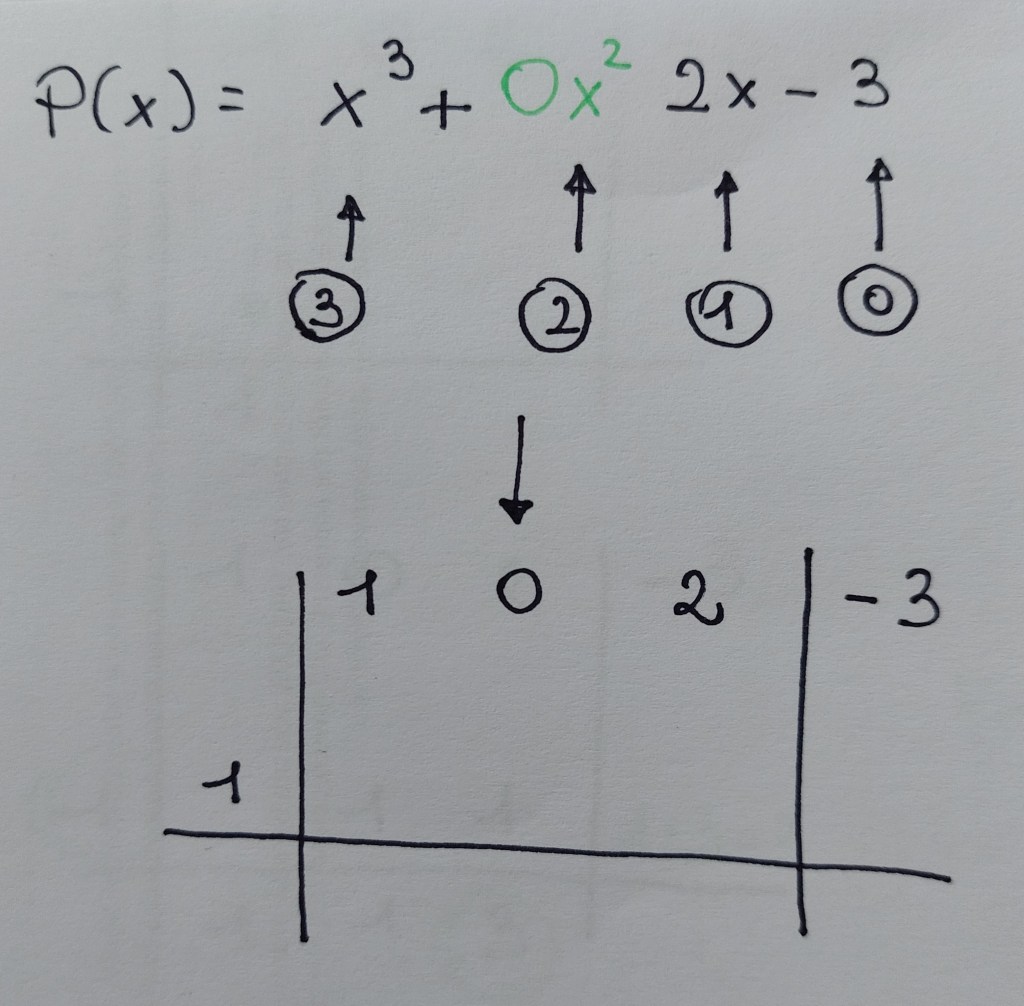
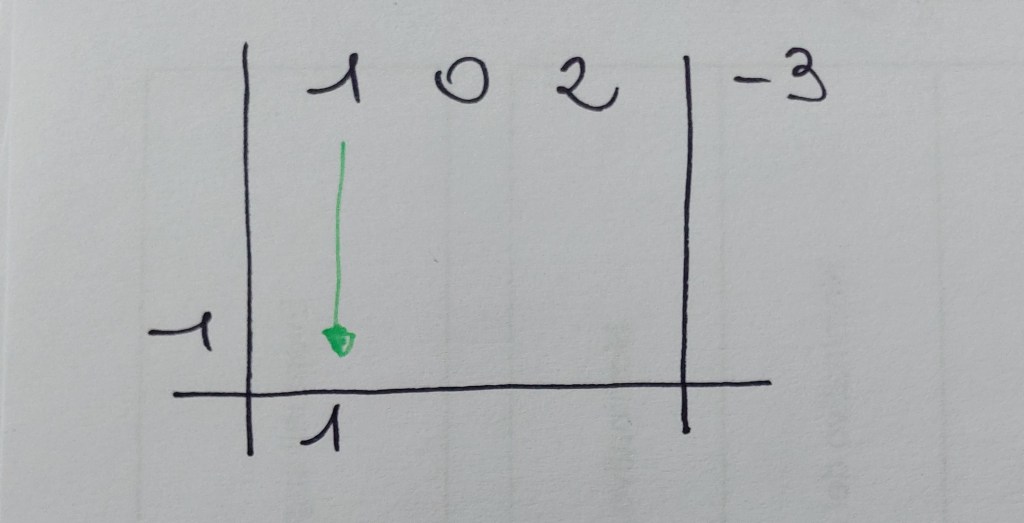
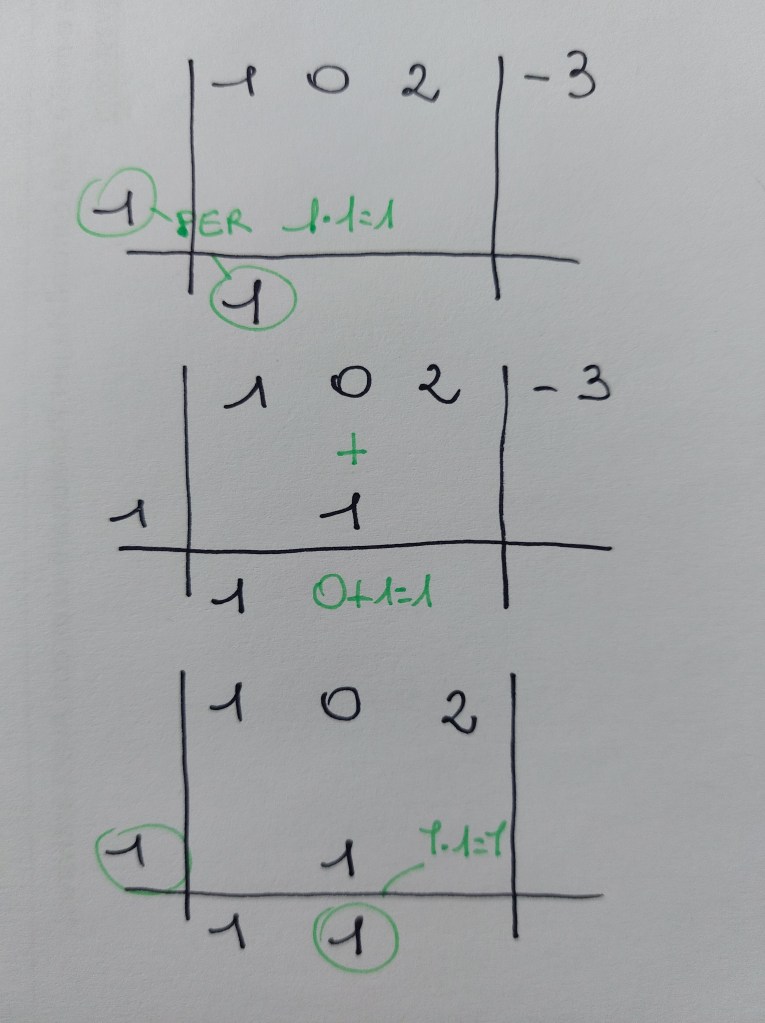
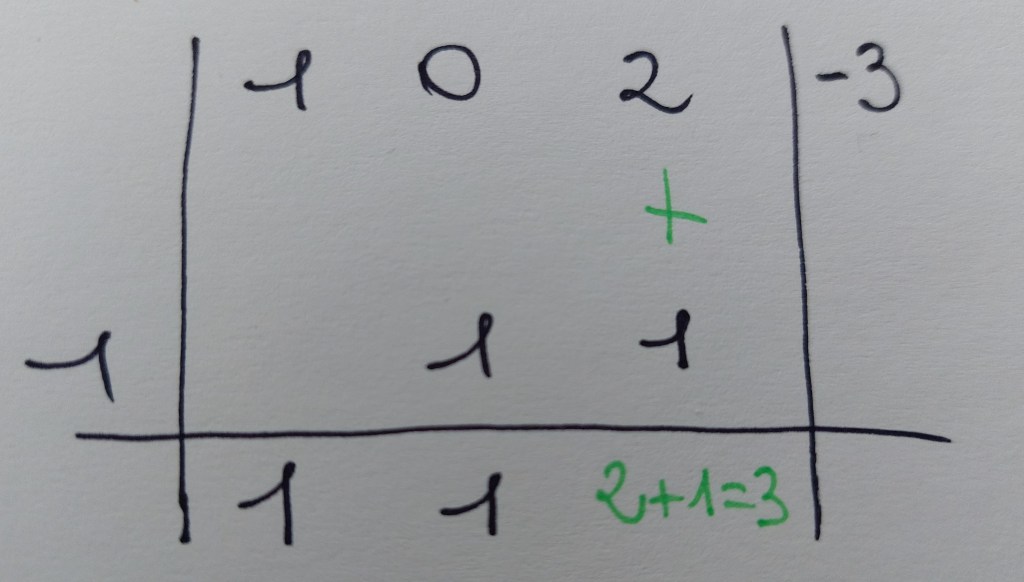
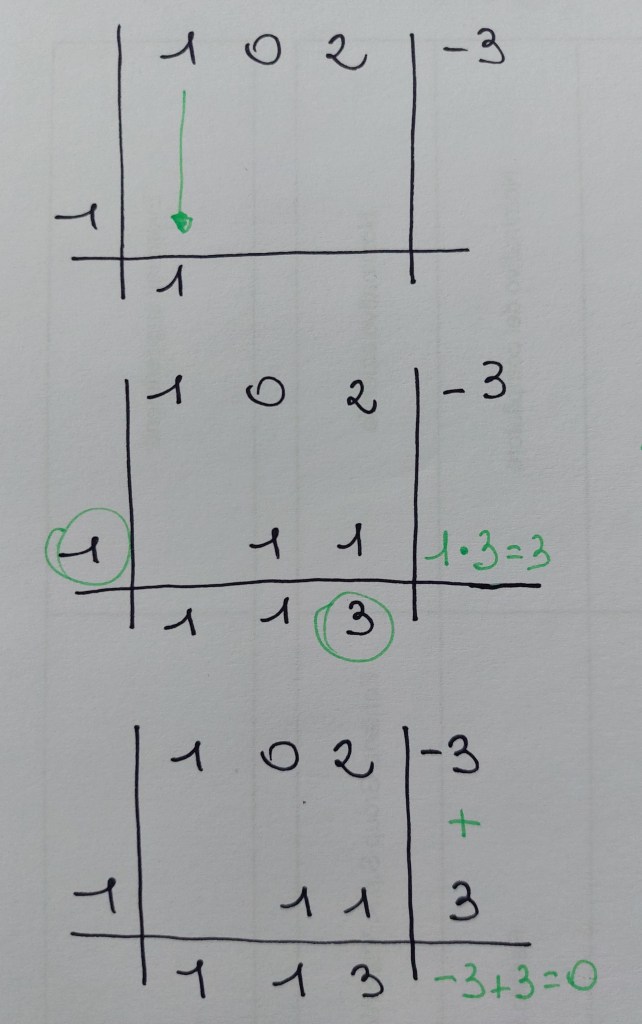
Nota: per sapere per quali binomi posso dividere bisogna usare il teorema di Ruffini:
un polinomio è divisibile per un binomio del tipo x – a soltanto se scambiando la sua incognita con l’opposto del termine noto del divisore viene annullato
Si fa la prova con tutti i termini che sono divisori del termine noto, se il coefficiente del termine di grado massimo è 1: quello che annulla il polinomio sostituendolo all’incognita è la radice.
