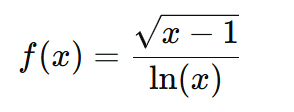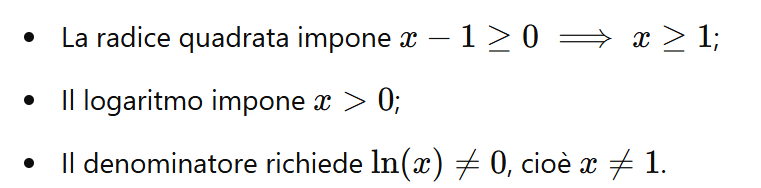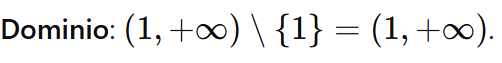In questo articolo c’è una panoramica dei principali casi in cui è necessario imporre condizioni per determinare il dominio di una funzione. Il dominio rappresenta l’insieme dei valori di x per i quali la funzione è definita.
Innanzitutto uno schema iniziale:
Attenzione alle funzioni con radicali, poiché in genere la presenza del radicale comporta che si debbano imporre condizioni solo se l’indice del radicale è pari.

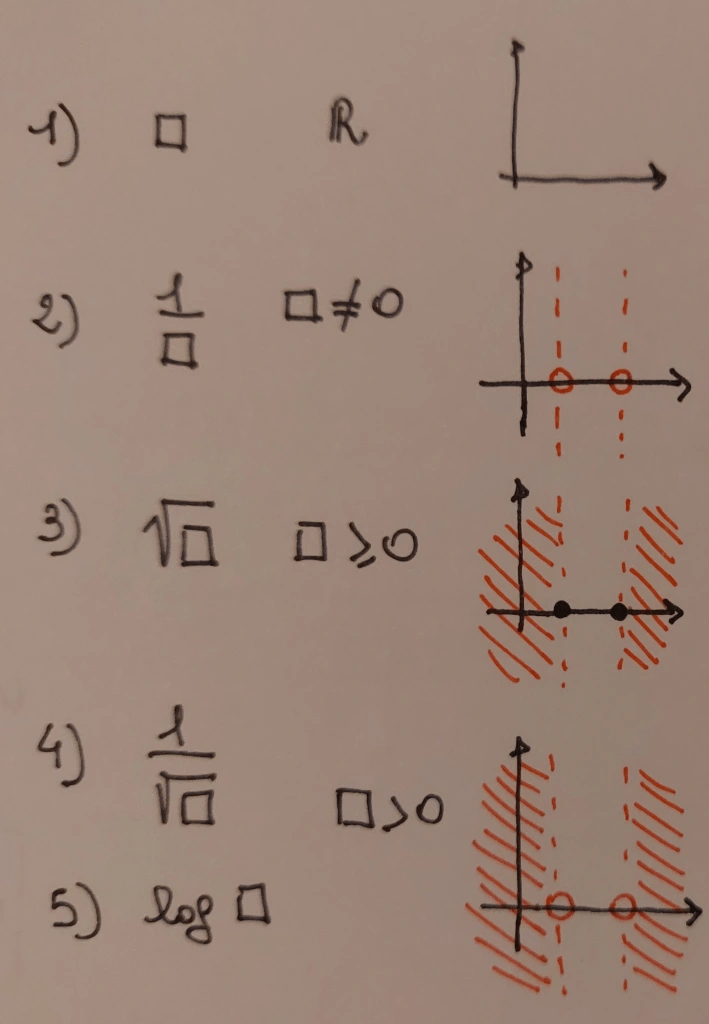
Analizziamo ora diversi casi di funzioni e di combinazioni di funzioni, partendo dalla funzione base:

1. Funzioni polinomiali con esponente intero e positivo

Non ci sono delle x al denominatore né sotto radice: non devo escludere nessun punto o intervallo dal dominio.
Condizione da imporre: nessuna

2. Funzioni con radici a indici dispari

Ci sono delle x sotto radice, ma le radici con indici dispari non costringono a imporre che l’argomento della radice sia positivo: non devo escludere nessun punto o intervallo dal dominio.
Condizione da imporre: nessuna

3. Funzioni con radici di indici pari
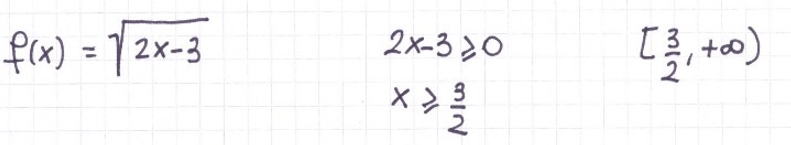
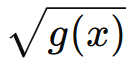
La radice quadrata (o in generale una radice pari) è definita solo per argomenti non negativi.
Quando ho una funzione con radice quadrata (o comunque con esponente pari) al numeratore, devo porre il radicando maggiore o uguale a zero. Devo escludere degli intervalli, ma gli estremi, in cui il radicando è proprio zero, non vengono esclusi.
Condizione da imporre:

Esempio:
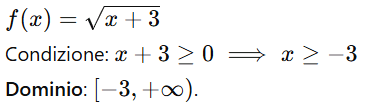
4. Funzioni razionali
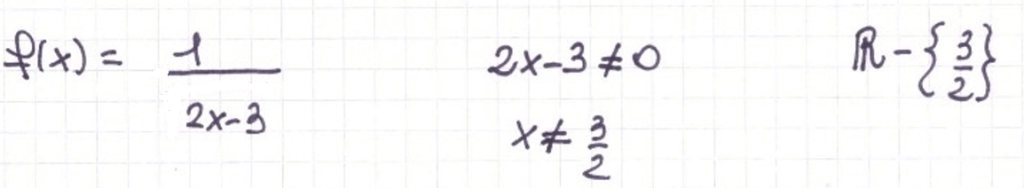
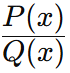
In questo caso ci sono delle x al denominatore): devo escludere quei punti per cui il denominatore si annulla. Non devo fare disequazioni per trovare intervalli, mi basta escludere dei valori puntuali, in modo che che il denominatore sia diverso da zero
Condizione da imporre:
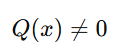
Esempio:
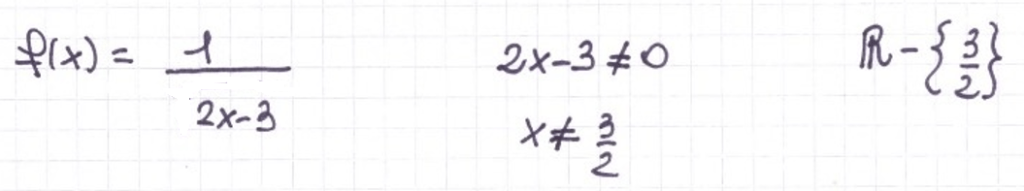
Esempio:

5. Funzioni razionali con radici al denominatore
Oltre a imporre che il denominatore sia diverso da zero, occorre distinguere due casi:
a) le radici hanno indici dispari: in questo caso è come se la radice non ci fosse, in quanto non implica condizioni in più

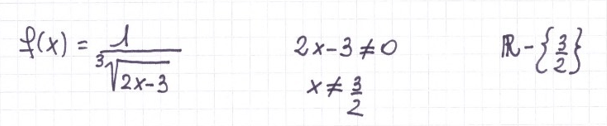
b) le radici hanno indici pari: in questo caso c’è in più la condizione che impone che quanto sta sotto radice sia positivo, oltre a essere diverso da zero
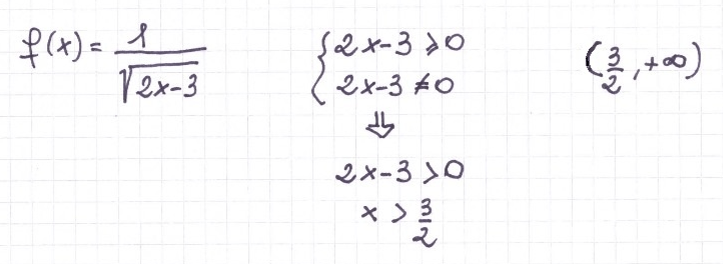
6. Funzioni logaritmiche

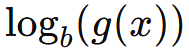
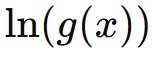
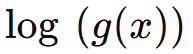
Il logaritmo è definito solo per argomenti positivi.
Condizione da imporre:

Esempio:
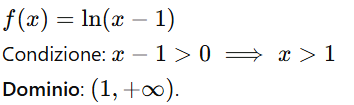
7. Funzioni esponenziali

Le funzioni esponenziali sono definite per tutti i numeri reali, quindi non richiedono condizioni particolari.
Esempio:
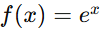

5. Funzioni trigonometriche
Le funzioni trigonometriche sin(x) e cos(x) non hanno restrizioni nel dominio (sono definite per ogni x∈R ). Tuttavia, alcune funzioni come la tangente o la cotangente non sono definite in corrispondenza di determinati valori.
Esempio:
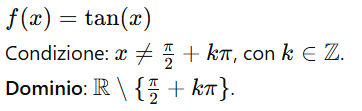

RIEPILOGHI:
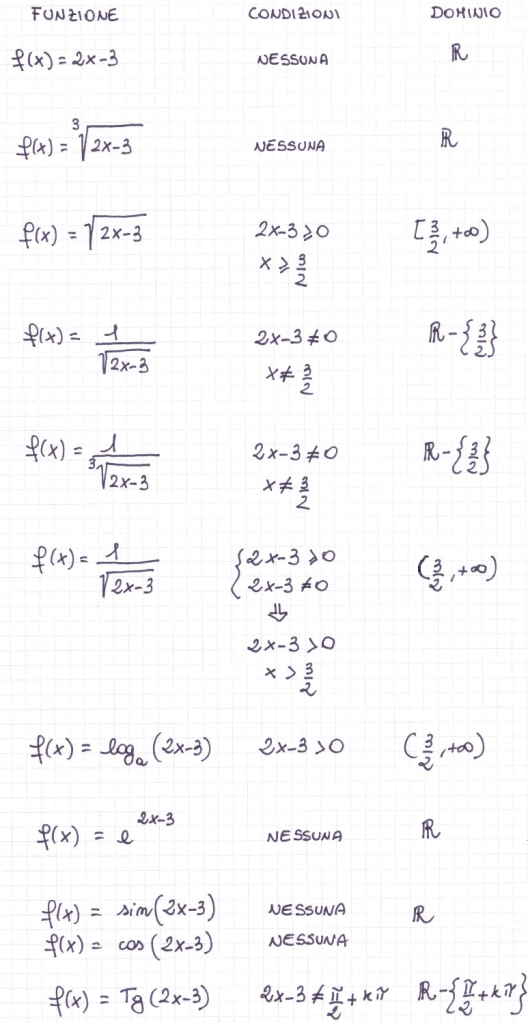
Altre funzioni composte
Quando una funzione combina più tipi di termini (razionali, radici, logaritmi, ecc.), si devono considerare contemporaneamente valide tutte le condizioni
Esempio:
funzione con radice quadrata al denominatore o con logaritmo: il radicando o l’argomento del logaritmo vanno posti strettamente maggiori di zero. Devo escludere degli intervalli e gli estremi, in cui il radicando o l’argomento del logaritmo è proprio zero, vengono esclusi.
4. Funzioni composte razionali e con radici con indici pari
Esempio:

Esempio: