Logaritmi ed eaponenziali sono strettamente connessi.
La crescita esponenziale è ripidissima, così come quella logaritmica è una delle meno ripide.
Per capire l’entità della crescita esponenziale fare riferimento a questo articolo.
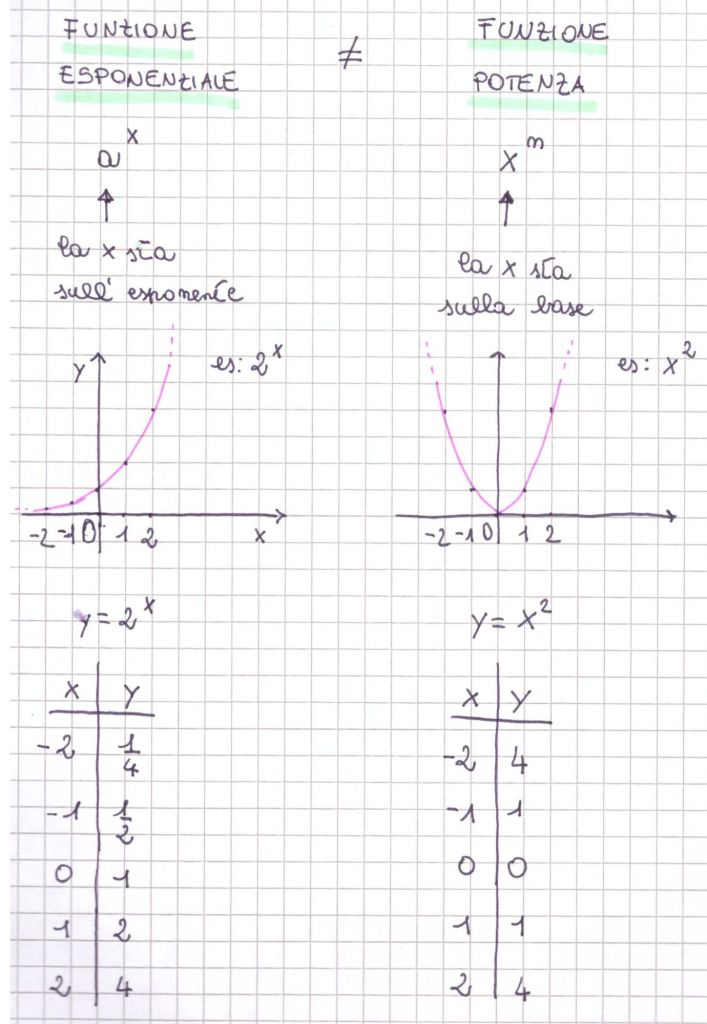
La funzione esponenziale si differenzia dalla funzione potenza, in quanto la x non sta sulla base, ma sull’esponente: questo fa sì che l’andamento di queste due funzioni sia completamente diversa.
La parola “logaritmo” deriva dalle due parole greche λόγος (logos), che significa ragione, proporzione, relazione (la stessa radice di “logica”) e ἀριθμός (arithmós) che significa numero, quindi sta a significare “il numero relativo” o “il numero in relazione a”.
Il logaritmo è la funzione inversa dell’esponenziale: una delle conseguenze di ciò è che, mentre il risultato della funzione esponenziale non è mai minore di zero o uguale a zero, così il logaritmo non si può fare su quantità che siano minori o uguali a zero.

Il significato matematico del logaritmo è: l’esponente da dare a una base in modo che il risultato sia pari all’argomento.
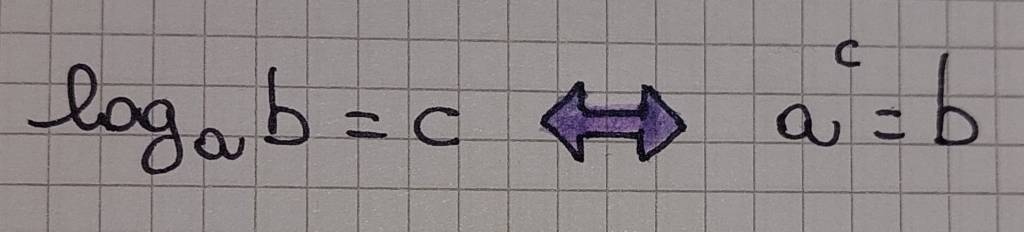
Di seguito a è la base, b l’argomento e c il logaritmo.
Ad esempio 2 è il logaritmo in base 3 di 9, perché 3 elevato a 2 dà 9.

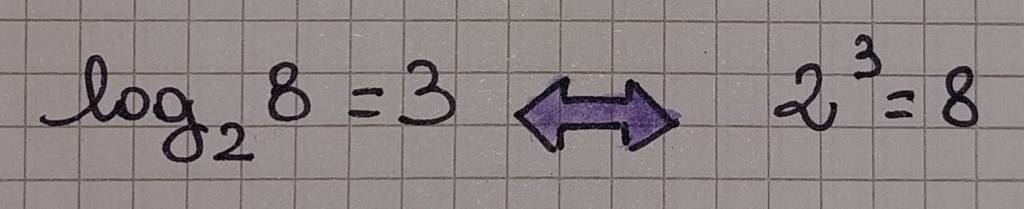
Invece 3 è il logaritmo in base 2 di 8, perché 2 elevato a 3 dà 8.
Se log è scritto senza che vi sia indicata la base, allora è implicito che la base sia 10.
Se invece si trova scritto ln vuol dire che il logaritmo ha come base il numero di Nepero e, con valore approssimativo 2,71.
Lo scozzese Nepero, che dà il nome alla costante e, fu anche colui che scoprì i logaritmi.
I logaritmi servono per poter esprimere numeri molto grandi in modo immediato, infatti, se consideriamo i numeri naturali 0, 1, 2, 3, 4, 5, 6, 7, 8 e i numeri 1, 2, 4, 8, 16, 32, 64, 128, 256, notiamo che i primi sono i logaritmi in base 2 dei secondi.
I logaritmi possono servire anche a svolgere i calcoli in modo semplificato, ad esempio se vogliamo calcolare il risultato della moltiplicazione di 8 e 32 possiamo farlo facendo l’addizione tra i logaritmi 3 e 5 e poi applicando la potenza 8 al 2 (infatti 28=256=23+5).
È utile ricordare che:
- un numero elevato a una potenza negativa equivale al reciproco dello stesso numero elevato al valore assoluto della potenza
- un numero sotto radice n-sima equivale allo stesso numero elevato alla 1 diviso n
Per risolvere i logaritmi occorre ricordare bene le proprietà delle potenze e dei radicali, oltre alle proprietà del logaritmi.
Questa espressione logaritmica ad esempio:
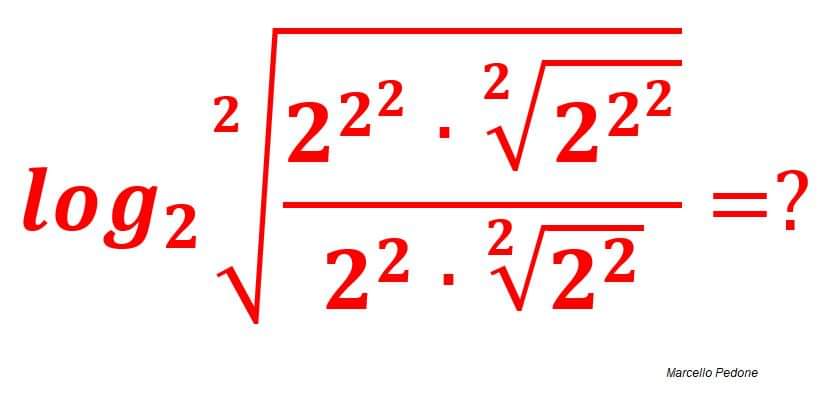
si risolve così
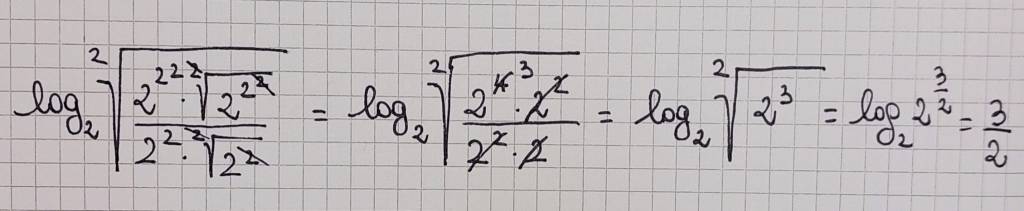
Di seguito un riassunto delle formule più utili delle equazioni logaritmiche o che si risolvono con i logaritmi.

Di seguito un documento con altri schemi e informazioni utili per risolvere semplici esercizi su esponenziali e logaritmi.

