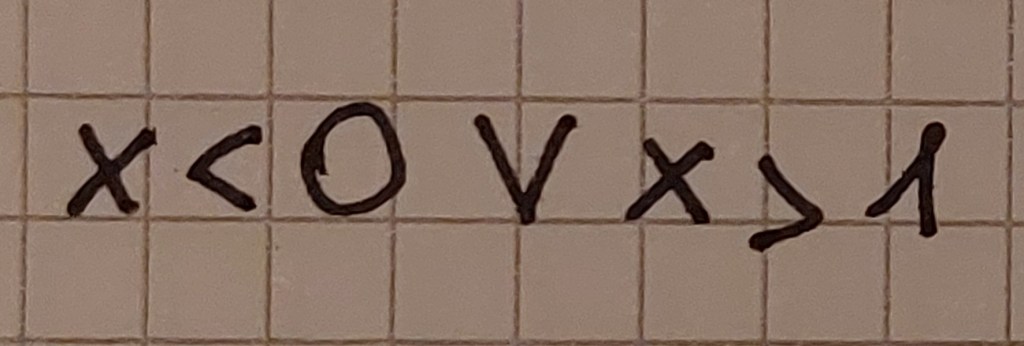
Gli errori più comuni nel risolvere le disequazioni secondo la mia esperienza sono i seguenti:
1) moltiplicare o dividere a destra e a sinistra per una quantità minore di zero e non invertire il verso della disequazione. Per evitare questo errore ricordiamoci che se si moltiplica una disuguaglianza per una quantità minore di zero ciò che era minore diventa maggiore e viceversa, ad esempio:
2 < 5
-2 > -5
2) scambiare il procedimento che si usa per le disequazioni di primo grado con quello che si usa per le disequazioni di secondo grado. Per evitare questo errore leggiamo il seguente approfondimento.
Le disequazioni di primo grado si riferiscono al grafico di una retta e l’equazioni ad esse associate possono avere al massimo un’intersezione con l’asse delle x, quindi risolverle è abbastanza semplice, basta portare i termini con le x a sinistra e quelli senza x a destra:

Il che graficamente corrisponde all’intervallo, illimitato a destra, dei valori delle x che si trovano a destra di 3/2.
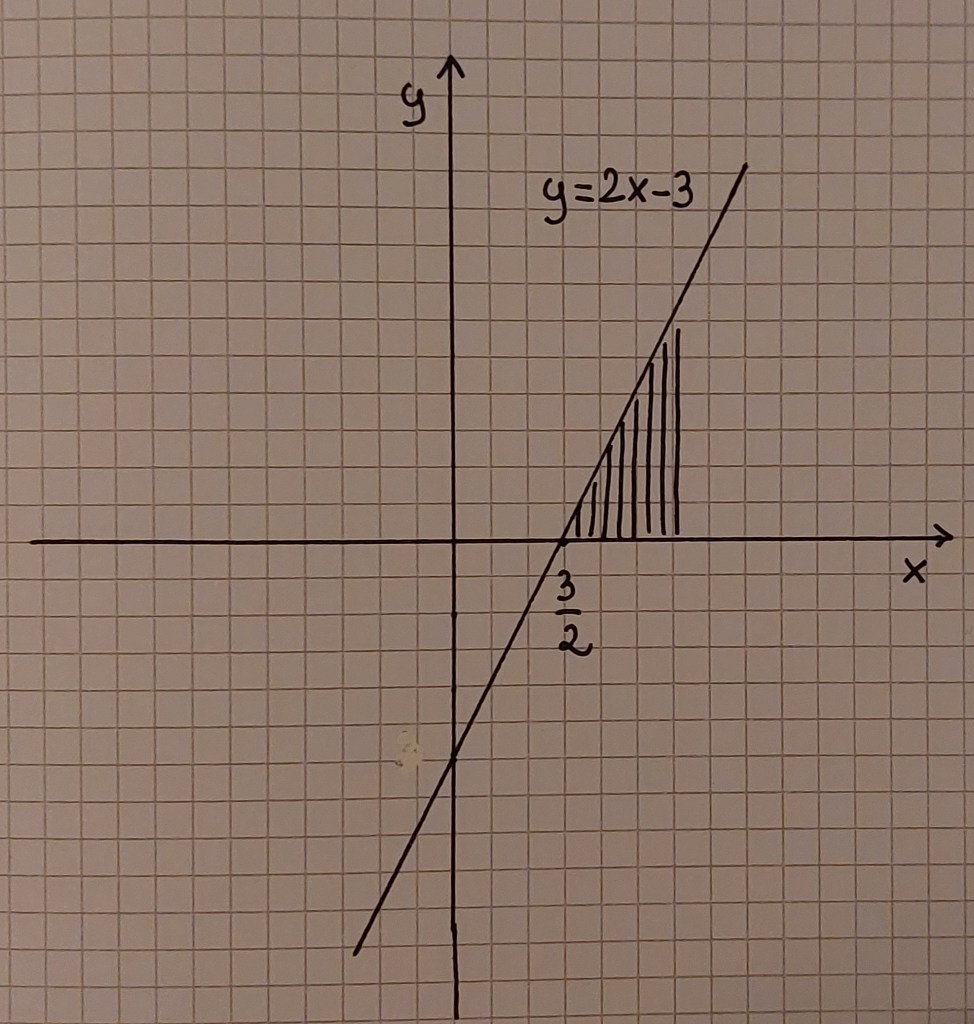
Se ci troviamo davanti a un’equazione di terzo grado che presenta solo il termine di grado 3 e il termine noto la soluzione è abbastanza simile: basta portare il termine senza la x a destra e fare la radice cubica a destra e a sinistra e si troverà un unico intervallo illimitato come soluzione, che in questo caso corrisponde con le x maggiori di 2:
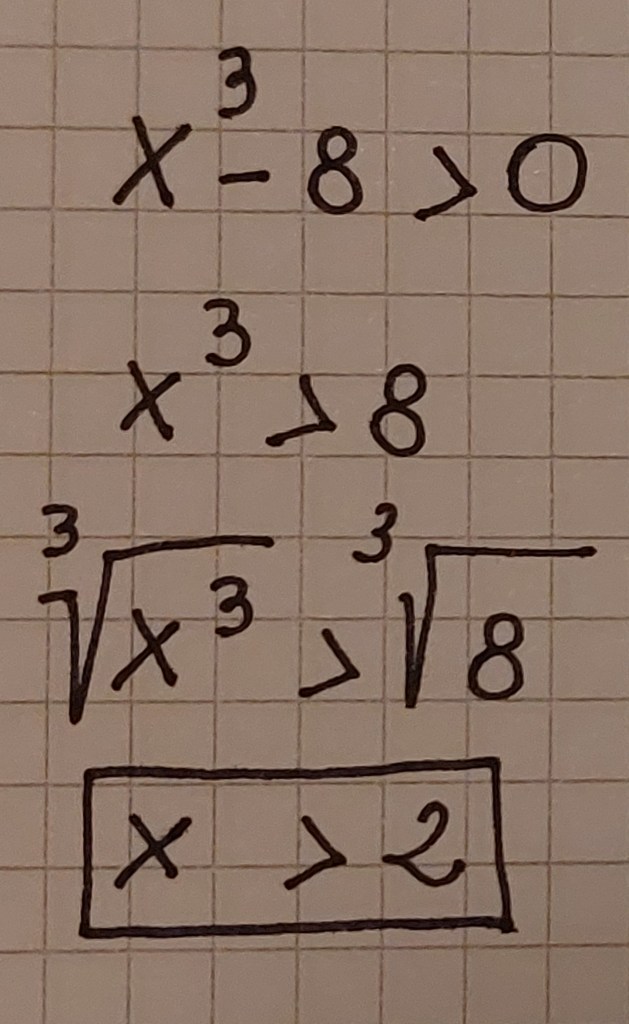
Graficamente:
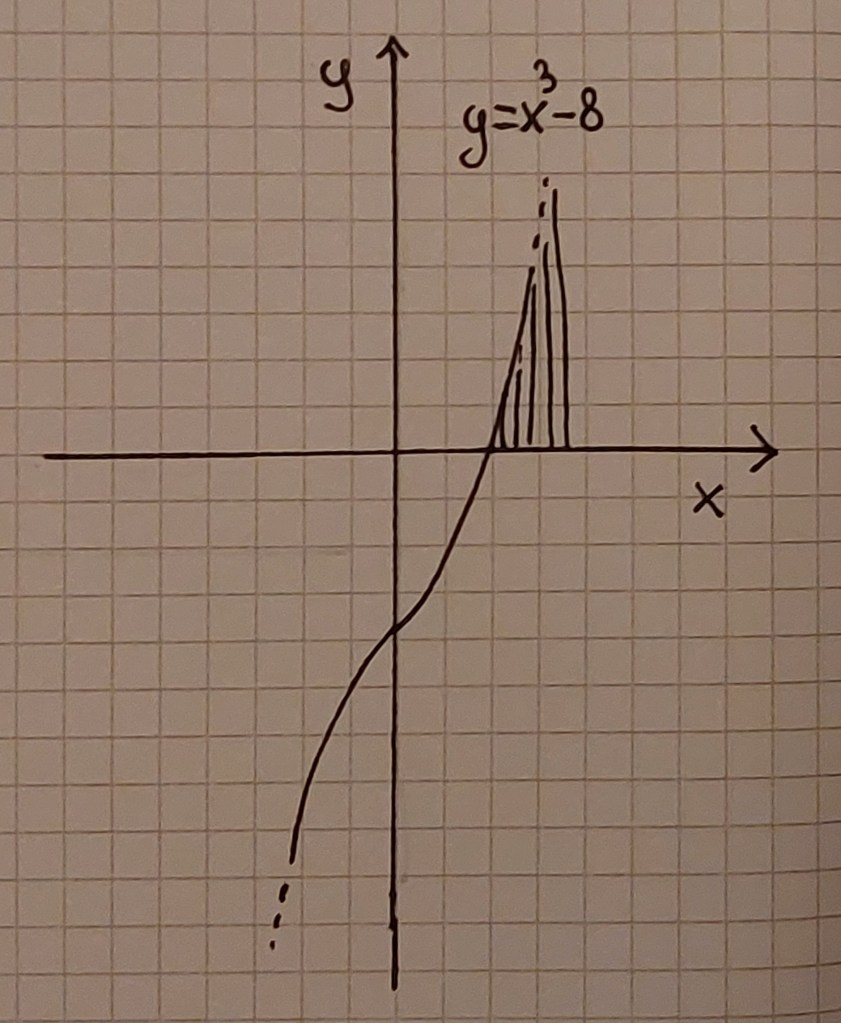
La situazione è del tutto diversa nel caso delle equazioni di grado 2: in questo caso, infatti, le soluzioni di un’equazione di secondo grado possono essere al massimo due, pertanto l’individuazione degli intervalli che sono soluzioni della disequazione è più complessa che nei casi appena visti.
Per tale motivo è obbligatorio mettere la disequazione in forma implicita, risolvere l’equazione associata con la formula risolutiva del delta, trovare le soluzioni, che possono essere due, una o nessuna a seconda che il delta sia maggiore, uguale o minore a zero, e poi scegliere gli intervalli da prendere come soluzione in base al segno del coefficiente del termine di secondo grado, in genere denominato “a” (che se è positivo indica una concavità verso l’alto e se è negativo verso il basso).
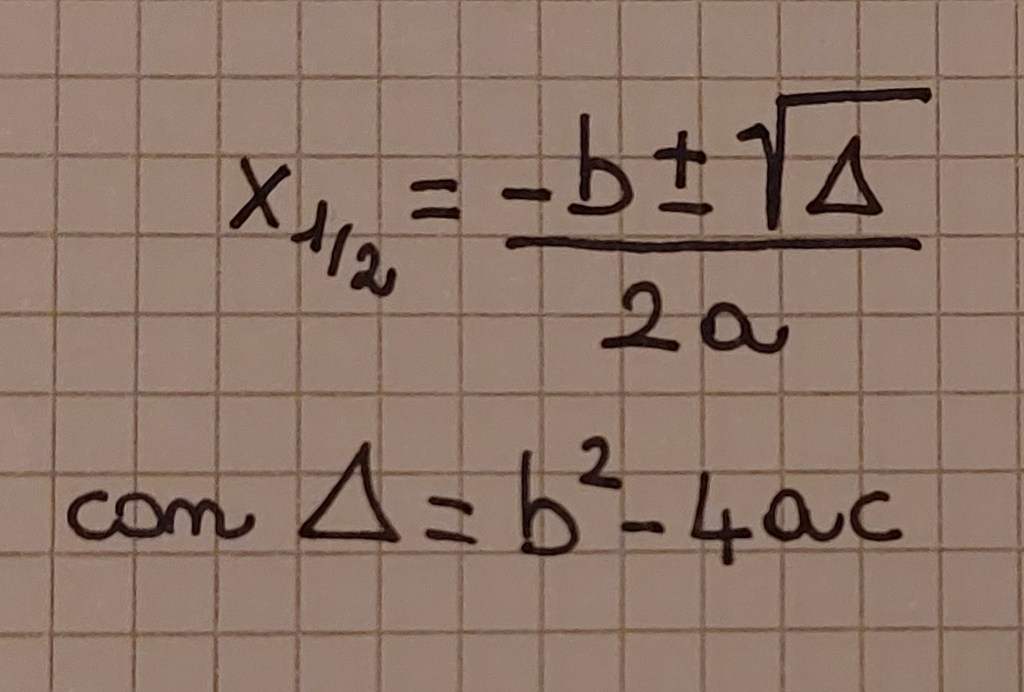
Solo se l’equazione è pura o spuria, si possono usare le formule risolutive semplificate (attenzione però, si tratta sempre di formule che prevedono l’individuazione di due potenziali soluzioni e non permettono di evitare la discussione della concavità e della posizione della parabola).
La tentazione di portare il termine noto a destra e di fare semplicemente la radice quadrata a destra e a sinistra può essere forte, specialmente quando l’equazione è pura, ma è sbagliato, perché così non si considerano le due soluzioni delle equazioni di secondo grado.
Il caso seguente ad esempio presenta proprio un’equazione associata pura:

Nel caso in esame la concavità è verso l’alto, quindi si prendono i valori esterni.
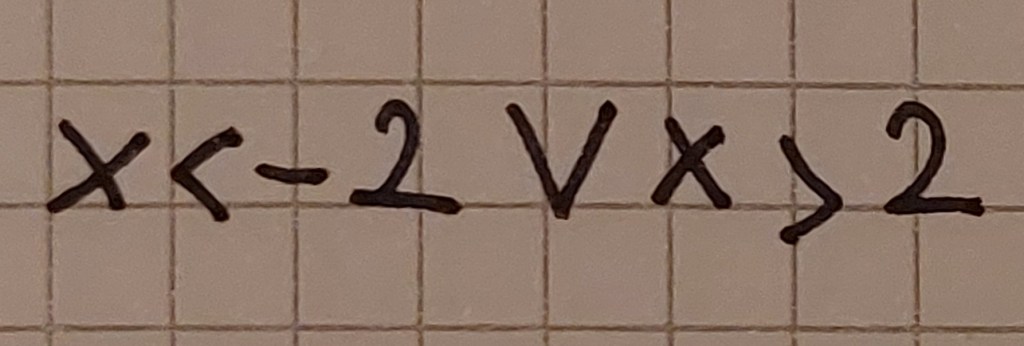
Graficamente si può rappresentare così (disegno non in scala):
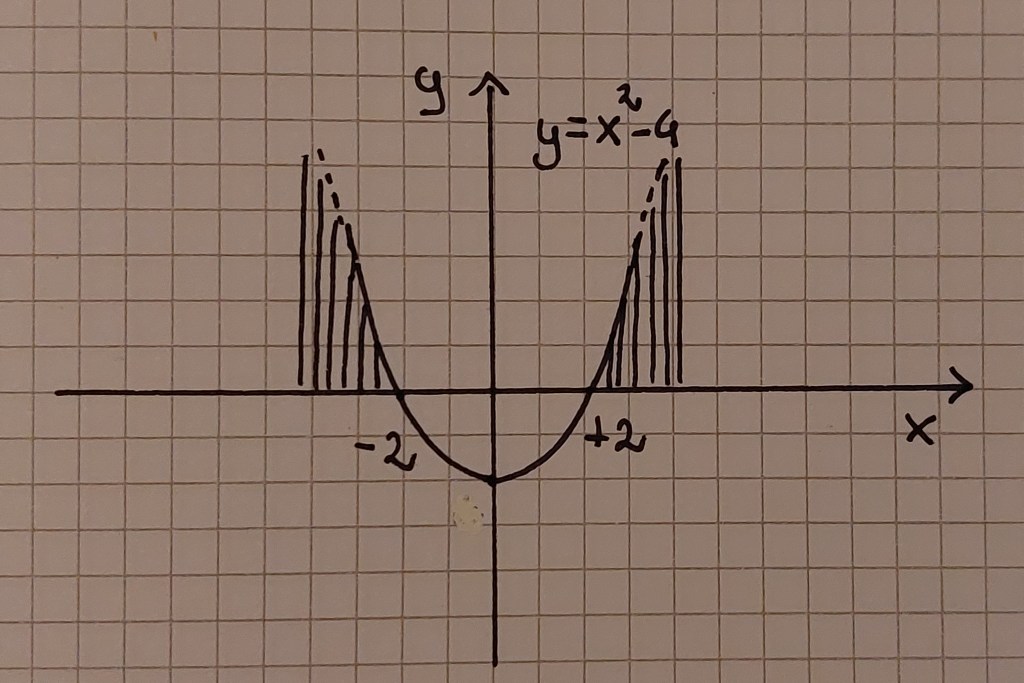
3) non riconoscere equazioni di secondo grado. Questo può succedere quando ad esempio ci troviamo una disequazione in questa forma:
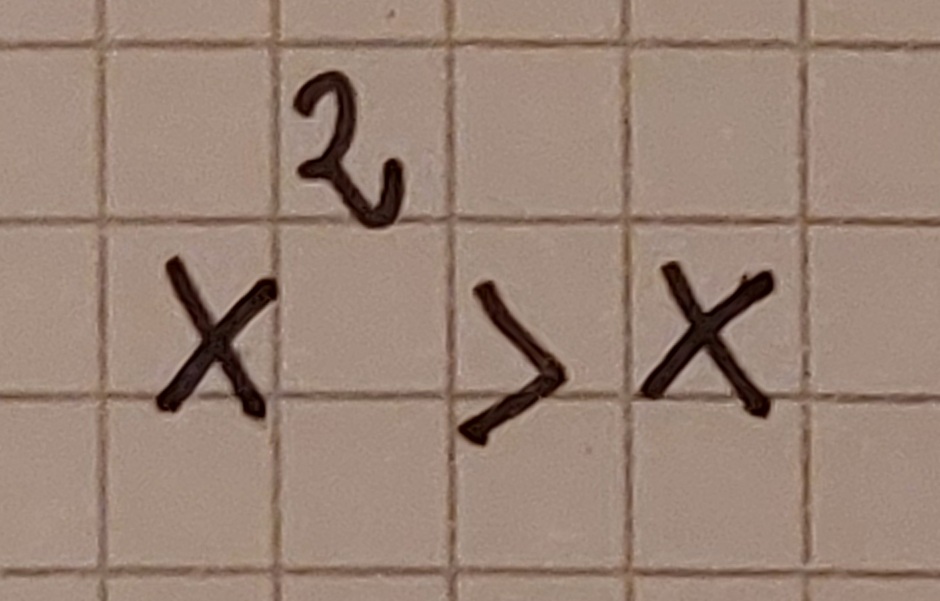
La tentazione potrebbe essere quella di dividere a destra e sinistra per x (errore grave, perché non sappiamo se x è diversa da 0, caso in cui sarebbe impossibile dividere, e non sappiamo se è negativa, caso in cui dovremmo invertire il verso della disequazione. Il procedimento corretto prevede di individuare prima di tutto l’equazione associata, portando la x a sinistra:
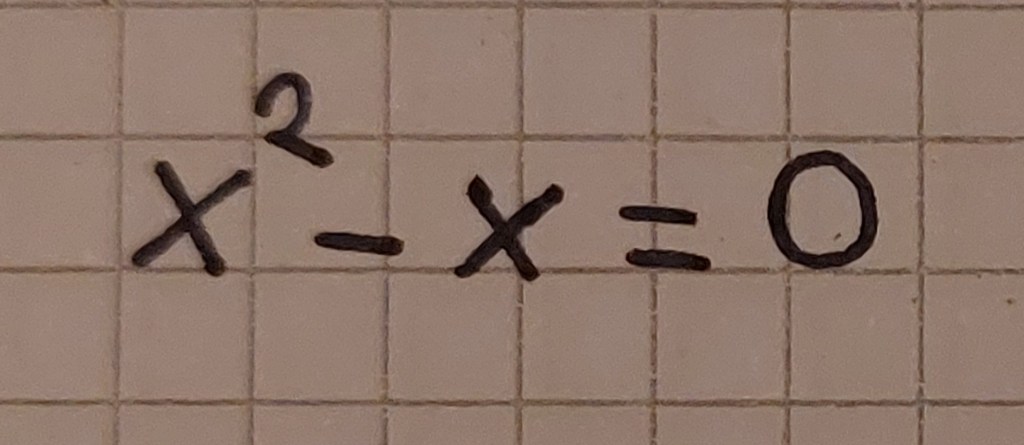
In questo caso si tratta di una spuria, che si può risolvere raccogliendo la x e considerando la legge di annullamento del prodotto, per cui le soluzioni sono 0 e 1:

Essendo la concavità anche in questo caso verso l’alto prendiamo i valori esterni: