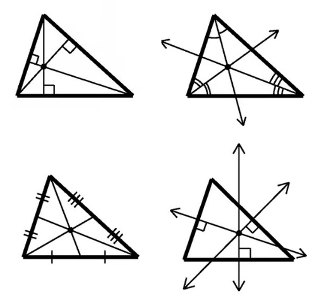
Ortocentro (H) = intersezione delle altezze del triangolo (altezza = segmento perpendicolare tracciato da ciascun vertice al lato opposto o al suo prolungamento).
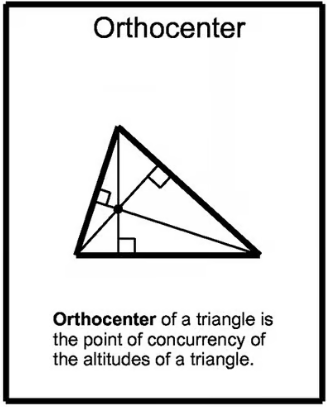
- Interno se il triangolo è acutangolo.
- Esterno se è ottusangolo.
- Nel caso di triangolo rettangolo coincide con il vertice dell’angolo retto.
Incentro (I) = intersezione delle bisettrici degli angoli interni (bisettrice = retta che taglia a metà l’angolo).
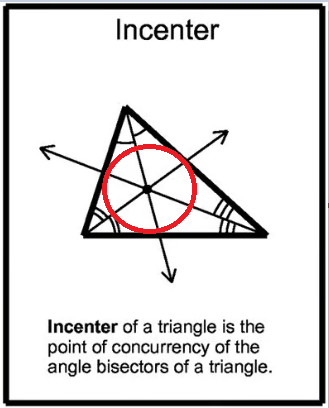
- Sempre interno al triangolo;
- Equidistante dai lati;
- Centro del cerchio inscritto.
Baricentro (G) = intersezione delle mediane (mediana = segmento che congiunge il vertice al punto medio del lato opposto).
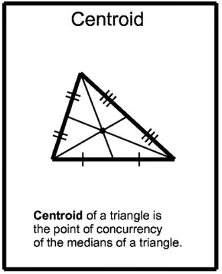
- Sempre interno al triangolo;
- Detti A(xA, yA), B(xB,yB) e C(xC,yC) i vertici del triangolo, si ha:
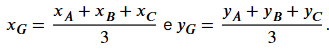
Circocentro (O) = intersezione degli assi dei lati (asse di un segmento = perpendicolare al lato condotta sul suo punto medio, cioè sul punto medio tra i suoi estremi).
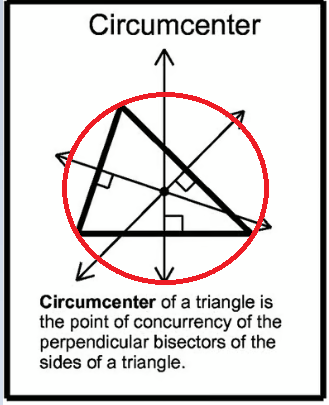
- Interno se il triangolo è acutangolo;
- Esterno se è ottusangolo.
- Equidistante dai vertici;
- Centro del cerchio circoscritto.
Retta di Eulero = linea che passa per ortocentro (H), baricentro (G) e circocentro (O).
Nel triangolo equilatero tutti i punti coincidono, in quello isoscele si trovano tutti sulla stessa retta (la mediana=bisettrice=altezza=asse relativa al lato diverso dagli altri).
