L’equazione di Fisher è una relazione fondamentale in macroeconomia e finanza che collega il tasso d’interesse nominale i, il tasso d’interesse reale r e il tasso di inflazione π. Questa equazione, sviluppata dall’economista americano Irving Fisher, viene utilizzata per analizzare l’impatto dell’inflazione sui tassi di interesse e per stimare il rendimento reale degli investimenti.
L’equazione di Fisher si esprime generalmente come:
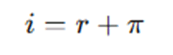
dove:
- i è il tasso d’interesse nominale,
- r è il tasso d’interesse reale,
- π è il tasso di inflazione (se è quello atteso in particolare è meglio specificare πe)
A seconda dell’inflazione attesa ex-ante, si stima il tasso di interesse nominale da applicare negli investimenti, affinché il rendimento reale non sia maggiore o minore di quello dovuto in assenza di inflazione.
Infatti, con un’inflazione maggiore di zero la moneta perde valore e così i creditori, se si lasciasse il tasso di inflazione pari a r, andrebbero a incassare meno di quanto dovrebbero, con un’inflazione minore di zero (deflazione) andrebbero a incassare di più.
Per cercare di evitare questi squilibri si stima un tasso di inflazione, detto πe (la “e” sta per expected) e in base a quello si stima il tasso di interesse nominale i, in modo che il tasso di interesse sia pari a r:
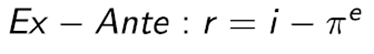
Il tasso reale che poi si verifica effettivamente con l’inflazione effettiva è invece:
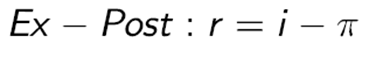
Questo implica che, in un contesto di inflazione, quindi, il rendimento nominale deve essere più elevato per compensare la perdita di potere d’acquisto.
Se l’inflazione ex post (quella effettiva) risulta maggiore dell’inflazione attesa, si verificano diversi effetti economici e redistributivi:
- Per i debitori e i creditori: questo scenario favorisce i debitori e penalizza i creditori. I debitori restituiranno il denaro preso in prestito con un valore reale inferiore rispetto a quello previsto inizialmente, poiché l’inflazione ha eroso il potere d’acquisto. In altre parole, il denaro che restituiscono vale meno di quanto ci si aspettasse.
- Per i salariati: se i salari non vengono adeguati automaticamente all’inflazione, i lavoratori potrebbero subire una riduzione del potere d’acquisto. Ciò potrebbe portare a una perdita reale del reddito se i salari non crescono al ritmo dell’inflazione effettiva.
- Per gli investitori: gli investimenti con tassi di interesse nominali fissati (come obbligazioni a tasso fisso) perdono valore reale. Gli investitori, quindi, subiscono una perdita in termini di potere d’acquisto poiché i rendimenti sono inferiori rispetto al livello dell’inflazione effettiva.
- Politiche monetarie: un’inflazione effettiva superiore a quella attesa può portare le autorità monetarie ad adottare misure restrittive per ridurre la pressione inflazionistica, come l’aumento dei tassi di interesse. Tuttavia, l’effetto dipenderà dalla reattività dell’economia e dalla capacità delle politiche di controllo.
- Redistribuzione della ricchezza: in generale, un’inflazione ex post superiore a quella attesa può comportare una redistribuzione della ricchezza dai creditori ai debitori e può influenzare i bilanci familiari, i profitti aziendali e le decisioni di investimento e risparmio.
Questa situazione può generare incertezza economica, poiché rende difficile per le imprese e i consumatori fare previsioni accurate sui prezzi futuri, influenzando quindi il comportamento di spesa e investimento.
Se l’inflazione ex post (effettiva) risulta inferiore a quella attesa, si verificano alcuni effetti importanti:
- Per i debitori e i creditori: Questo scenario avvantaggia i creditori e sfavorisce i debitori. I debitori devono restituire il denaro preso in prestito con un valore reale maggiore rispetto a quanto previsto. Il potere d’acquisto del denaro che devono restituire è infatti superiore rispetto a quello atteso, poiché l’inflazione più bassa non ha eroso il valore reale del debito come previsto.
- Per i salariati: Se i salari sono stati negoziati sulla base dell’inflazione attesa, possono risultare più alti rispetto a quanto sarebbe necessario per mantenere il potere d’acquisto. I lavoratori potrebbero quindi beneficiare di una capacità di acquisto più elevata rispetto a quanto stimato.
- Per gli investitori: Gli investitori che hanno acquistato obbligazioni o altri strumenti finanziari a tasso fisso beneficiano di un ritorno reale maggiore rispetto a quello previsto. La loro rendita non viene erosa dall’inflazione come si aspettavano, aumentando il valore reale dei loro investimenti.
- Politiche monetarie: Un’inflazione effettiva inferiore a quella attesa può portare le autorità monetarie a rivedere la loro politica, potenzialmente adottando misure espansive (come la riduzione dei tassi di interesse) per stimolare l’inflazione e incoraggiare la crescita economica.
- Redistribuzione della ricchezza: L’effetto redistributivo è l’opposto di quello che si verifica con un’inflazione superiore a quella attesa. In questo caso, la ricchezza tende a spostarsi dai debitori ai creditori, poiché il valore reale del denaro che i debitori devono restituire è maggiore di quanto avevano previsto.
In generale, un’inflazione ex post inferiore a quella attesa può causare difficoltà ai debitori, riducendo la loro capacità di ripagare i prestiti, e può influenzare negativamente la domanda e la crescita economica, poiché le persone e le imprese potrebbero essere meno inclini a spendere e investire in un contesto di bassa inflazione.
Ricavare l’equazione di Fisher
Per ricavare l’equazione di Fisher, partiamo dalla relazione tra il tasso di interesse nominale e reale in un contesto di inflazione:
Relazione tra potere d’acquisto reale e nominale:
Immaginiamo di avere un pane che non ammuffisce mai e di fare un investimento senza usare i soldi, ma usando delle quantità di pane, il cui valore non cambia con l’inflazione. Il nostro investimento avrà valore pari a P e un anno dopo a P aumentato del tasso di interesse reale, quindi P+P⋅r = P(1+r).
Immaginiamo ora invece di avere un investimento iniziale di P in moneta e di ottenere un rendimento pari al tasso nominale i. Dopo un anno, il valore dell’investimento sarà P(1+i) e per indicarne l’effettivo potere di acquisto lo rapportiamo al per il prezzo atteso del pane l’anno dopo, cioè per il prezzo aumentato dell’inflazione.
Uguagliando le due quantità e semplificando per P a destra e a sinistra si ottiene:
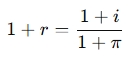
L’equazione sopra può essere scritta come:
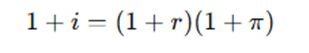
Espandendo il prodotto sul lato destro:
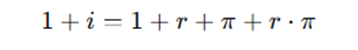
Se r e π sono relativamente piccoli, il termine r⋅π diventa trascurabile, e quindi possiamo approssimare l’equazione come:

