Lo studio di una funzione può essere suddiviso in vari passaggi. Ecco una guida generale:
1) DOMINIO: insieme di tutti i valori di x per i quali la funzione è definita
Nota operativa: in genere, se non ci sono denominatori, logaritmi, tangenti e radici con indice pari il dominio è composto da tutti i reali)
2) subito dopo aver definito il dominio imposto il DISEGNO DEL GRAFICO DELLA FUNZIONE cancellando o mettendo pallini vuoti nei punti esclusi
3) SIMMETRIE: pari o dispari.
Nota operativa: calcolo f(-x):
se viene = f(x) è pari
se viene = –f(x) è dispari
se viene diversa sia da f(x) che da –f(x) non è né pari né dispari
4) INTERSEZIONI CON ASSI: x e y.
Nota operativa: Il primo sistema (quello con y=0) si risolve per confronto e il secondo (quello con x=0) per sostituzione.
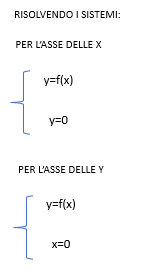
Nota operativa: il primo sistema può dare più di una soluzione, il secondo può dare al massimo solo una soluzione.
Nota operativa: se nel primo sistema una delle soluzioni è l’origine (0,0) allora è inutile fare il secondo sistema, perché l’origine è già un’intersezione con l’asse delle y e può essercene solo una
5) RIPORTO LE INTERSEZIONI come pallini pieni sul grafico
6) CALCOLO IL SEGNO facendo il grafico dei segni
Per studiarlo:
- Pongo la funzione maggiore a 0
- Risolvo la disequazione con il grafico dei segni
- Individuo gli intervalli in cui è positiva e quelli in cui è negativa,
7) RIPORTO IL SEGNO SUL GRAFICO, cancellando sul grafico i settori in cui la funzione non passa (la parte positiva se la funzione è negativa e viceversa)
8) CALCOLO I LIMITI PER CERCARE GLI ASINTOTI: per x che tende ai margini del dominio, sia da sinistra che da destra (anche a infinito se è il caso)
Facendo il limite per x che tende agli estremi del dominio che non sono più o meno infinito si ottengono gli asintoti verticali, mentre facendo il limite per x che tende a più o meno infinito si ottengono, se ce ne sono, gli asintoti orizzontali o quelli obliqui, a seconda che si verifichino le condizioni del seguente schema:
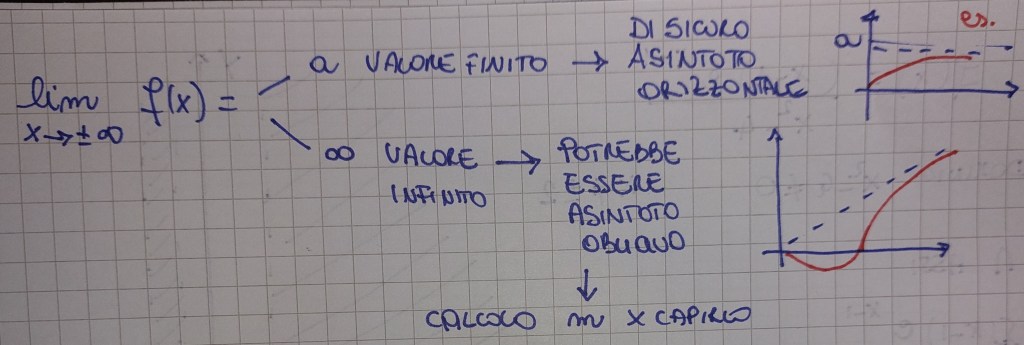
Se il limite è infinito c’è quindi la possibilità che esista l’asintoto obliquo, che è una retta del tipo y=mx+q, e quindi occorre trovare m e q:
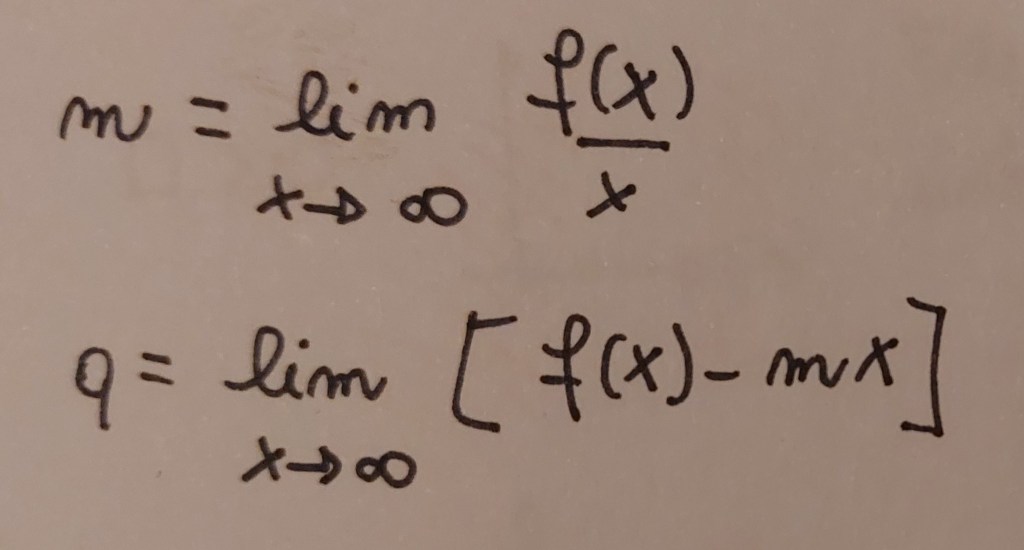
Continuità: verifica della continuità della funzione su tutto il suo dominio.
Derivate: calcolo delle derivate della funzione, che forniscono informazioni sul tasso di variazione istantaneo.
Punti Critici: determinando dove la derivata è uguale a zero o non definita.
Intervalli di crescita e decrescita della funzione: con l’analisi del segno della derivata.
Punti di Flesso: punti in cui la concavità della funzione cambia.
I seguenti schemi aiutano nel calcolo dei limiti.
Limiti per x che tende a infinito per le funzioni razionali fratte:

Gerarchia degli infiniti:


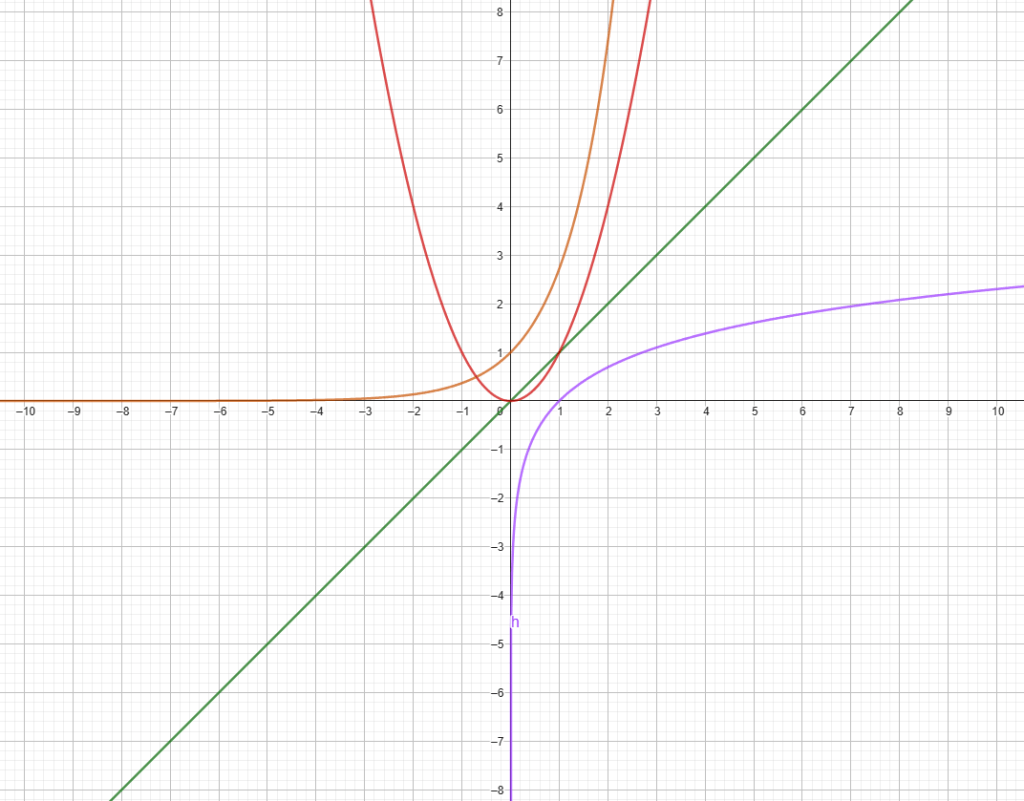
Grafico preso da Geogebra: