Gli intervalli in matematica possono servire per indicare le soluzioni di una disequazione o di un sistema di disequazioni, che a loro volta possono servire a indicare i domini di una funzione.
La base per capire gli intervalli sono le disuguaglianze usate per definirne gli estremi.

Possiamo avere intervalli limitati o illimitati.
Dati due numeri reali a e b, gli intervalli limitati indicano che la variabile può essere compresa tra due valori, uno all’estremo inferiore (il minimo valore che può assumere la variabile) e uno all’estremo superiore (il massimo valore che può assumere la variabile).
Poiché la retta dei reali è orientata, andando da sinistra verso destra si trovano numero che via via crescono:

Potremmo scrivere l’elenco dei numeri interi che troviamo in ordine da sinistra a destra separati dal segno di minore, perché leggendo la disuguaglianza da sinistra a destra, nell’ordine naturale, troviamo prima i numeri più piccoli e poi quelli più grandi, ad esempio così:
-7 < -6 < -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7
Se ad esempio dobbiamo indicare un intervallo compreso tra -2 e 3, consiglio di riportare prima i due estremi, lasciando uno spazio abbastanza largo per scrivere in mezzo:
-2 3
inseriamo poi la x in mezzo:
-2 x 3
e i segni di minore come è naturale metterli:
-2 < x < 3
Gli intervalli limitati sono indicati così in modo formale:
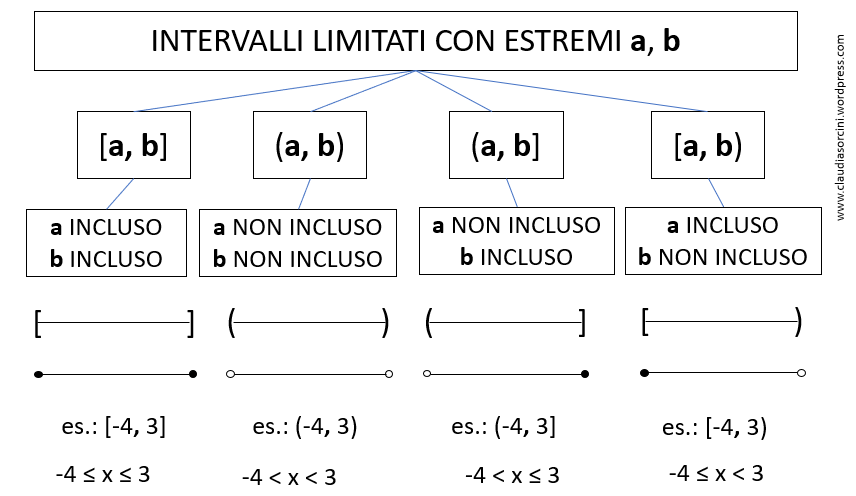
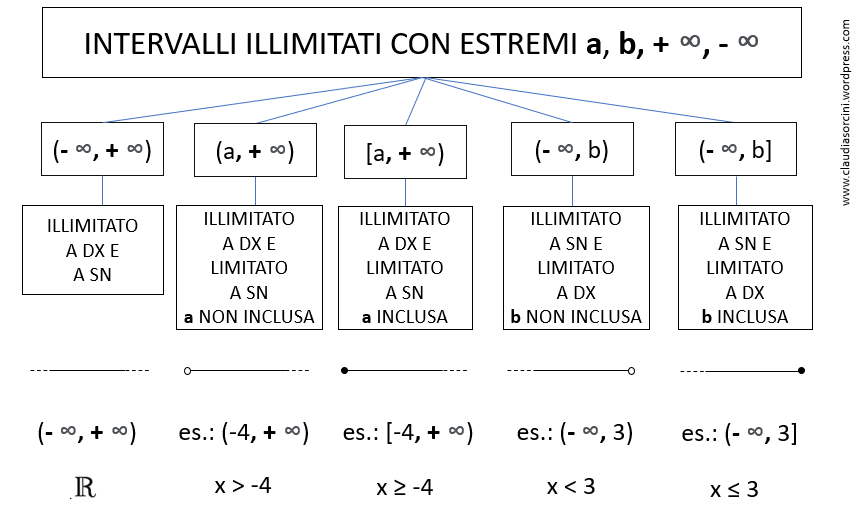
Mentre gli intervalli illimitati si possono indicare formalmente così: